pixabay.com
Brilio.net - Practicing mathematics questions consistently is an important step in preparation for the Test-Based National Selection (SNBT). Practicing math questions helps improve understanding and mastery of the math concepts required in the SNBT exam.
By repeating various types of questions, prospective test takers can deepen their understanding of basic mathematical concepts, expand their knowledge of various techniques and strategies for solving questions, and increase the speed and accuracy in solving questions.
One of the mathematics materials in the test includes permutation questions. Understanding the various levels of difficulty of permutation questions that can appear in UTBK, prospective exam participants can prepare themselves better.
They can focus on understanding basic concepts, practice intermediate problems, and also challenge themselves by trying to solve more complicated permutation problems. The more practice you do with various levels of difficulty, the more prepared the prospective exam takers will be to face the permutation questions in UTBK.
Below, brilio.net summarizes examples of permutation questions accompanied by explanations to help you in preparing for SNBT in 2024.
15 Examples of multiple choice questions about permutations and their discussion:

photo: pixabay.com
Question 1:
How many ways can the letters in the word "MATH" be arranged so that the vowels are not in order?
A. 720
B. 5040
C. 2880
D. 360
E. 1440
Discussion of Question 1:
The letters in the word "MATH" are 4 consonants (M, T, M, K) and 6 vowels (A, E, A, I, A). The total number of letters is 10. We want to count how many ways the vowels are not sequential. We can calculate it by mutating the 4 consonant letters first, then placing the 6 vowel letters between them. The number of ways is

photo: special
because we have 4 consonants and 7 positions between them.

photo: special
The total is 24 X 7 = 168, so the correct answer is D.
Problem 2:

photo: special
How many anagrams are possible from this set?
A. 60
B. 120
C. 20
D. 24
E. 10
Discussion of Question 2:
Anagrams are arrangements of words or sentences made from the letters of a word or sentence in a different order. In this case, we want to count how many ways there are to arrange the numbers in the set S. Since there are 5 numbers in the set, there are 5! method. So, the correct answer is D.
Question 3:
How many anagrams are possible for the word "CALCULUS"?
A. 5040
B. 10080
C. 720
D. 2520
E. 40320
Discussion of Question 3:
The word "CALCULUS" has 8 unique letters. Therefore, there are 8! how to arrange the letters. So, the correct answer is A.
Question 4:
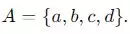
photo: special
How many subsets are possible from set A?
A. 16
B. 8
C. 4
D. 12
E. 32
Discussion of Question 4:
Each element in a set may or may not belong to a subset. Therefore, each element has 2 choices, namely entering or not entering. Since (A) has 4 elements, the number of possible subsets is
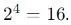
photo: special
So, the correct answer is A.
Question 5:
How many words can be made from the letters in the word "BALL", if there are no repeated letters in one word?
A. 24
B. 120
C. 60
D. 20
E. 10
Discussion of Question 5:
The word "BALL" has 4 unique letters. Therefore, there are 4! how to arrange the letters. So, the correct answer is A.
(Intern/Robiul Adil Robani)
Question 6:
A basketball team consists of 7 players. How many ways can there be 5 of the 7 players to be in the starting lineup?
A. 21
B. 35
C. 42
D. 70
E. 120
Discussion of Question 6:
We need to calculate the combination of 5 players out of a total of 7 players. The number of combinations is

photo: special
So, the correct answer is A.
Question 7:
How many three-digit numbers can be formed from the numbers 1, 2, 3, 4, and 5 if the same number can appear more than once?
A. 120
B. 125
C. 150
D. 100
E. 1000
Discussion of Question 7:
To form a three-digit number, we have 5 choices for each digit. Therefore, the total number is 5 X 5 X 5 = 125. So, the correct answer is B.
Question 8:
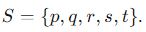
photo 8: special
How many permutations are possible from this set?
A. 120
B. 60
C. 20
D. 24
E. 5!

photo: pixabay.com
Discussion of Question 8:
In permutations, order matters. The number of permutations of a set S consisting of 5 elements is 5! or 120. So, the correct answer is A.
Question 9:
How many different ways can there be to arrange 5 books on a bookshelf?
A. 20
B. 60
C. 120
D. 720
Discussion of Question 9
To arrange 5 books on a bookshelf, we use the concept of permutation. The number of setting ways is 5! because there are 5 books arranged, and the order is important. Therefore, the correct answer is C.
Question 10:
A bookstore owner has 6 mathematics books, 4 physics books, and 3 chemistry books. If he wanted to display 3 books side by side in a shop window, how many different ways could he choose the books?
A. 288
B. 120
C. 60
D. 750
Discussion of Question 10
The number of mathematics, physics, and chemistry books owned by the shop owner are 6, 4, and 3 respectively. Because he wants to display 3 books side by side, we have to calculate the permutations for each type of book, then add them up. The sum is P(6.3) + P(4.3) + P(3.3). After counting, we get 6! + 4! +3! = 720 + 24 + 6 = 750. Therefore, the correct answer is D
Question 11:
How many different ways can the letters be arranged in the word "CALCULUS"?
A. 5040
B. 720
C. 2520
D. 840
Discussion of Question 11:
The word "CALCULUS" has 8 unique letters. The number of setting ways is 8! because each letter is considered unique and their order is important. Therefore, the correct answer is A.
Question 12:

photo: special
How many permutations are possible from this set?
A. 12
B. 24
C. 48
D. 4
Discussion of Question 12:
In permutations, order matters. The number of permutations of a set S consisting of 4 elements is 4! or 24. Therefore, the correct answer is B.
Question 13:
A band consists of 5 members. How many different ways can they be positioned in a row?
A. 20
B. 120
C. 240
D. 720
Discussion of Question 13:
To arrange the positions of the 5 band members in a row, we use the concept of permutation. The number of setting ways is 5! because there are 5 members and the order is important. Therefore, the correct answer is D.
Question 14:
How many anagrams are possible for the word "MATHEMATICS"?
A. 3628800
B. 1440
C. 720
D. 40320
Discussion of Question 14:
The word "MATHEMATICS" has 11 unique letters. The number of anagrams that can be made from this word is 11! because each letter is considered unique and their order is important. Therefore, the correct answer is A.
Question 15:
A teacher wants to select 3 students from his class to take part in a mathematics competition. If the class consists of 10 students, how many ways can the teacher select 3 students?
A. 30
B. 90
C. 120
D. 720
Discussion of Question 15:
We have to calculate the combination of 3 students out of a total of 10 students. The number of combinations is
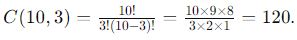
photo: special
Therefore, the correct answer is C.
(brl/lak)